Question

Paul and Betty are setting up a business to decorate skateboard decks. it costs $200 to hire the equipment and facilities. It costs an additional $20 for the paints for each board. They charge $50 to decorate a board. What is the cost equation in the form C = mx + c?What is the revenue equation in the form R = mx + c? at breakeven, cost = revenue how many boards do they need to decorate in order to break even?

Answer 1

Answer:

a) C = 20x + 200

b) R = 50x

The Break-even point is at (6.67, 333.33)

See the graph below

Step-by-step explanation:

Given:

The cost to hire equipment and facilities = $200

The cost to paint each board = $20

The charge per decoration = $50

To find:

the cost equation and revenue equation

break-even point using graph and equation

a) For the cost equation:

let the number of boards = x

The equation given for the cost equation is C = mx + c

where m = cost to paint each board = $20

c = cost to hire equipment and facilities = 200

The equation becomes:

`\begin{gathered} C\text{ = 20\lparen x\rparen + 200} \\ C=\text{ 20x + 200} \end{gathered}`

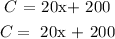
b) For the revenue equation:

let the number of boards decorated = x

The equation given for the revenue equation is R = mx + c

m = charge to decorate each board = $50

c = additional payment = 0

The equation becomes:

`\begin{gathered} R=\text{ 50\lparen x\rparen + 0} \\ R\text{ = 50x} \end{gathered}`

c) Plotting the 2 points for cost equation: C = 20x + 200

when x = 0

C = 20(0) + 200 = 200

C = 200

when x = 10

C = 20(10) + 200 = 200 + 200

C = 400

Plotting the 2 points for the revenue equation: R = 50x

when x = 0

R = 50(0)

R = 0

when x = 10

R = 50(10)

R = 500

d) Plotting the lines:

On the y-axis, each box represents 100 units

On the x-axis, each box represents 2 units

The 2 points for each equation are on the graph

e) Using the graph to get the break-even point;

The point of intersection of both equations will be the break-even point

Break-even point on the graph (x, y): (6.67, 333.33)

They need to decorate 6.67 boards to break even

f) At break-even, cost = revenue

To determine the number of boards they need to break even, we will equate the equation for the cost and the revenue

`\begin{gathered} C\text{ = R} \\ 20x\text{ + 200 = 50x} \end{gathered}`
`\begin{gathered} subtract\text{ 20x from both sides:} \\ 20x\text{ - 20x + 200 = 50x - 20x} \\ 200\text{ = 30x} \\ \\ divide\text{ both sides by 30:} \\ (200)/(30)=\text{ }(30x)/(30) \\ x\text{ = 6}(2)/(3) \end{gathered}`

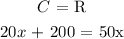
They need to decorate 6.67 boards to break even

when x = 6 2/3 = 6.67

R = 50(6 2/3) = 333.33

C = 20(6 2/3) + 200 = 333.33

Hence, the break-even point is (6.67, 333.33)