Question

The International Space Station is in a 300-mile-high orbit.Part AWhat is the station's orbital speed? The radius of Earth is 6.37×106m, its mass is 5.98×1024kg.Express your answer with the appropriate units.Part BWhat is the station's orbital period?Express your answer in minutes.

Answer 1

Part A

We will use the next formula to calculate the speed

`v=\sqrt[]{(G\cdot M)/(R)}`

where v is the speed, G is the gravitation constant, M is the mass and r is the radius

First, we need to convert the miles to meters

1 mile =1609m

Height of the orbit = 300 miles= 482700 m

The radius of the Earth = 6.37x10^6m

The radius of the Orbit, R = 6.37x10^6+482700=6852700m

M=5.98x10^24 kg

G= 6.673 × 10-11 N.m^2 / kg^2

Then we substitute

`v=\sqrt[]{((6.673*10^(-11))(5.98*10^(24)))/(6852700)}=7630.98\text{ m/s}`

Part B

For the period T

`T=(2\pi R)/(v)`

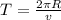
We substitute the values

`T=\frac{2\pi(6852700)}{7630.98\text{ }}=5642.4s`

ANSWER

Part A

7630.98 m/s

Part B

5642.4 s