Part A
We will use the next formula to calculate the speed
![v=\sqrt[]{(G\cdot M)/(R)}](https://img.qammunity.org/2023/formulas/physics/college/1vt8aizsks4v4nvddpb2a2whp6tap6rge1.png)
where v is the speed, G is the gravitation constant, M is the mass and r is the radius
First, we need to convert the miles to meters
1 mile =1609m
Height of the orbit = 300 miles= 482700 m
The radius of the Earth = 6.37x10^6m
The radius of the Orbit, R = 6.37x10^6+482700=6852700m
M=5.98x10^24 kg
G= 6.673 × 10-11 N.m^2 / kg^2
Then we substitute
![v=\sqrt[]{((6.673*10^(-11))(5.98*10^(24)))/(6852700)}=7630.98\text{ m/s}](https://img.qammunity.org/2023/formulas/physics/college/ttj574s11s9q2d0uq13d6bpi6ah5tvzo92.png)
Part B
For the period T
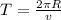
We substitute the values
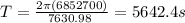
ANSWER
Part A
7630.98 m/s
Part B
5642.4 s