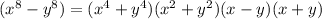Answer:
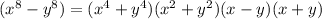
Step-by-step explanation:
Here, we want to factor the polynomial completely
To do this, we will engage the use of the difference of two squares
We apply this rule to even exponents
We have it as follows:
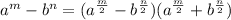
This is the law we are going to apply to factor the polynomial
We have this as follows:
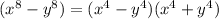
We can further split the even exponents with negative between them as follows:
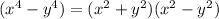
Finally, we split the even exponent with negative as follows:
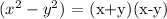
Thus, in cumulative, we have it as: