Question

Problem Set B: For #1 and #2, solve the equation using the guide of the boxes, then confirm that your solution is correct using the graph provided. 1. Solve xl - 2 = 3x + 2 2. Solve (2x - 11 -2 = -x

Answer 1

Question 1:

Adding 2 to both sides of the equation gives

`|x|=3x+4`

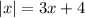
Now, the absolute value decomposes the above equation into two separate equations

`\begin{gathered} x=3x+4 \\ x=-3x-4 \end{gathered}`

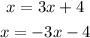
The first equation gives

`\begin{gathered} x=3x+4 \\ -2x=4 \\ \boxed{x=-2} \end{gathered}`

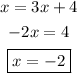
The second equation gives

`\begin{gathered} x=-3x-4 \\ 4x=-4 \\ \boxed{x=-1} \end{gathered}`

The graph of the system is

We see that the solutions exists at x =-1.

Question 2.

Adding 2 to both sides of the equation gives

`|2x-1|=-x+2`

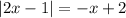
Decomposing the absolute value on LHS gives us two equations

`\begin{gathered} -(2x-1)=-x+2 \\ 2x-1=-x+2 \end{gathered}`

Solving the first equation gives

`\begin{gathered} 2x-1=x-2 \\ x=-1 \end{gathered}`

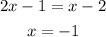
Solving the second equation gives

`\begin{gathered} 2x-1=-x+2 \\ 3x=3 \\ x=1 \end{gathered}`

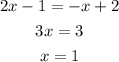
Hence, the solution to the equation is

`x=\pm1`

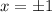
The graph of the solutions is

We see that the solution is at x = -1 and x = 1; hence, our solution is confirmed.