Question

Decide whether each statement is true. if false, demonstrate why:

Answer 1

Note that :

n! = n(n-1)(n-2)(n-3)...(2)(1)

Example :

3! = 3(2)(1) = 6

4! = 4(3)(2)(1) = 24

5! = 5(4)(3)(2)(1) = 120

From a. :

`\begin{gathered} (9!)/(3)=\frac{9*8*7*6*5*4*\cancel{3}*2*1}{\cancel{3}} \\ =9*8*7*6*5*4*2 \end{gathered}`

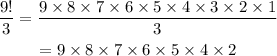
which is obviously not equal to 3! = 3 x 2 x 1 = 6

So, "a" is false

From b :

`\begin{gathered} (9!)/(8!)=\frac{9*\cancel{8*7*6*5*4*3*2*1}}{\cancel{8*7*6*5*4*3*2*1}} \\ =9 \end{gathered}`

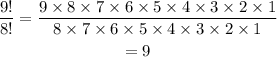
which is also obvious that it is not equal to 9! = 9 x 8 x 7 x ... x 1

So, "b" is also false

From c :

`\begin{gathered} (9!)/(4!5!)=\frac{9*8*7*6*\cancel{5*4*3*2*1}}{4*3*2*1*\cancel{5*4*3*2*1}} \\ =\frac{9*8*7*\cancel{6}}{4*\cancel{3*2}*1} \\ =(9*8*7)/(4*1) \\ =(504)/(4) \\ =126 \end{gathered}`

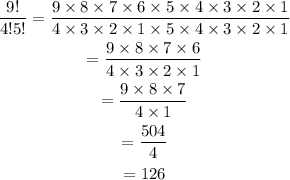
Since the result is equal to 126, therefore c. is TRUE

The cancel symbol, it is used when the numerator and the denominator has the same value.

For example :

`(ab)/(b)=\frac{a\cancel{b}}{\cancel{b}}=a`

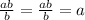
ab/b will result to a

Lets try an example :

when a = 2

b = 3

`(2(3))/(3)=(6)/(3)=2`

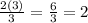
It is the same as :

`\frac{2\cancel{(3)}}{\cancel{3}}=2`

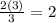
It is like multiplying 2 x (3/3) = 2 x (1) = 2