Note that :
n! = n(n-1)(n-2)(n-3)...(2)(1)
Example :
3! = 3(2)(1) = 6
4! = 4(3)(2)(1) = 24
5! = 5(4)(3)(2)(1) = 120
From a. :

which is obviously not equal to 3! = 3 x 2 x 1 = 6
So, "a" is false
From b :
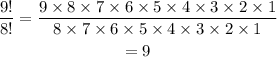
which is also obvious that it is not equal to 9! = 9 x 8 x 7 x ... x 1
So, "b" is also false
From c :
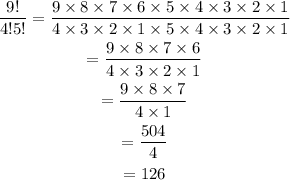
Since the result is equal to 126, therefore c. is TRUE
The cancel symbol, it is used when the numerator and the denominator has the same value.
For example :
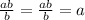
ab/b will result to a
Lets try an example :
when a = 2
b = 3
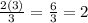
It is the same as :
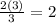
It is like multiplying 2 x (3/3) = 2 x (1) = 2