Question

What is the equation of the parabola in vertex form? 0=y2 - x - 4y+ 3 갈 2 O A. (x+12) = (y-4) f O B. (x – 3) =(y-2) OC O c. (x+1)=(y-2) O d. (x - 1)=(y+2)

Answer 1

Given equation:

The general expression for a parabola equation in vertex form:

`y^2\text{ =4ax}`

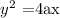
Where the axis of the parabola is the x-axis and the origin is zero

Writing the equation in vertex form takes the following steps:

1. Re-arrange the equation:

`\begin{gathered} y^2-x-4y+3\text{ = 0} \\ y^2-4y\text{ - x + 3 = 0} \end{gathered}`

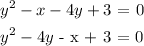
Factoring out:

`(y-2)^2-4\text{ -x + 3 = 0}`

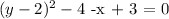
Re-arranging further:

`(y-2)^2\text{ = (x+1)}`

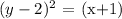
Hence, the equation of the parabola is Option C