Question

Use special right triangles to find the value of the variables no decimal answers. 30 60 90

Answer 1

Hello there. To solve this question, we have to remember some properties about special right triangles.

Given the following right triangles, we want to determine the measures of the missing sides (the variables):

For these triangles, we'll use the rule for the special 30-60-90 right triangles.

Given a triangle as mentioned, its sides follow the rule:

So for the first triangle, notice we were given the measure of the hypotenuse (the side opposite to the 90º angle) and we have to determine the values for x and y, the legs of the triangle.

Notice that y is opposite to the angle measuring 60º, which means that x is the side that is opposite to the angle measuring 30º.

In this case, we find that

`x=(32)/(2)=16`

And

`y=16√(3)`

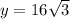
Using the rule mentioned above.

For the next triangle, we have one of the sides opposite to the angle measuring 60º and want to determine the missing leg and hypotenuse of the triangle (variables a and b).

For this, we know that

`12=a√(3)`

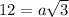
Dividing both sides of the equation by sqrt(3), we get

`a=(12)/(√(3))=(12√(3))/(3)=4√(3)`

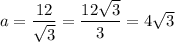
And the hypotenuse is then given by

`b=2a=2\cdot4√(3)=8√(3)`

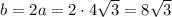
The final answer to this question is:

`\begin{gathered} x=16 \\ y=16√(3) \\ a=4√(3) \\ b=8√(3) \end{gathered}`

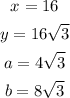
You can check that they satisfy the Pythagorean Theorem.