The area of a sector of a circle is ½ r² ∅, where r is the radius and ∅ the angle in radians subtended by the arc at the centre of the circle. So in the below diagram, the shaded area is equal to ½ r² ∅ . We also have that
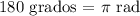
For thus we have that the angle 260 in radians is
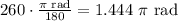
So the area of that sector is
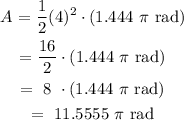
The answer is 11.5555 pi rad.