Question

Some experts believe that 23% of all freshwater fish in a country have such high levels of mercury that they are dangerous to eat. Suppose a fish market has 200 fish tested, and 48 of them have dangerous levels of mercury. Test the hypothesis that this sample is not from a population with 23% dangerous fish, assuming that this is a random sample. Use a significance level of 0.05. determine the z-test statistic, find the p-value, does the conclusion support or reject the null hypothesis

Answer 1

We have the proportion of the freshwater fish is

`\begin{gathered} p_0=23\% \\ p_0=0.23 \end{gathered}`

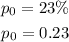
Now, from the sample we have the proportion

`\begin{gathered} p=(48)/(200) \\ p=0.24 \end{gathered}`

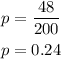
To test the hypothesis, we have

`\begin{gathered} H_0\colon p_0=0.23 \\ H_1\colon p_0\\e0.23 \end{gathered}`

We have

`\alpha=0.05,n=200`

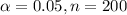
The test statistics

`z=\frac{p-p_0}{\sqrt[]{(p_0(1-p_0))/(n)}}`

Substituting the parameters, we obtain

`\begin{gathered} z=\frac{p-p_0}{\sqrt[]{(p_0(1-p_0))/(n)}} \\ z=\frac{0.24-0.23}{\sqrt[]{(0.23(1-0.23))/(200)}} \\ z=\frac{0.01}{\sqrt[]{(0.23*0.77)/(200)}} \\ z=0.3360514064 \end{gathered}`

Therefore, the test statistics is

`z=0.336\text{ (to thr}ee\text{ decimal places)}`

To find the P - value

Using the table, the p - value for the z score of 0.336 is

`\begin{gathered} p-value=0.736871 \\ p-value=0.7369\text{ (to four decimal places)} \end{gathered}`

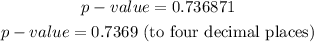
Notice that

`p-value=0.7369>0.05=\alpha`

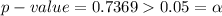
Therefore, since the p -value is greater than the level of significance, we fail to reject the null hypothesis, That is we support the null hypothesis