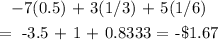Question

A game uses a single 6-sided die. To play the game, the die is rolled one time, with the following results: Even number = lose $71 or 3 = win $35 = win $10What is the expected value of the game?State your answer in terms of dollars rounded to the nearest cent (hundredth).

Answer 1

The expected value of the game is -$1.67

Step-by-step explanation:

Here, we want to get the expected value of the game

Each win results in an addition while each loss result in a minus

The numbers on a die are 1,2,3,4,5 and 6

The even numbers are 2,4,6 while the odd numbers are 1,3 and 5

To get the expected value, we multiply the probability and the value, then add up for all the probabilities given

For even numbers, the probability is 3/6 = 1/2 (the count of even numbers divided by the total count of numbers on the die)

The probability to get 1 is 1/6. The probability to get 3 is 1/6

The probability to get 3 or 1 is the sum of these two which is 1/6 + 1/6 = 2/6 = 1/3

To get a 5, rtrtthe probability is 1/6

The expected value is thus:

`\begin{gathered} -7(0.5)\text{ + 3(1/3) + 5(1/6)} \\ =\text{ -3.5 + 1 + 0.8333 = -\$1.67} \end{gathered}`