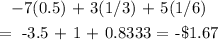Answer:
The expected value of the game is -$1.67
Step-by-step explanation:
Here, we want to get the expected value of the game
Each win results in an addition while each loss result in a minus
The numbers on a die are 1,2,3,4,5 and 6
The even numbers are 2,4,6 while the odd numbers are 1,3 and 5
To get the expected value, we multiply the probability and the value, then add up for all the probabilities given
For even numbers, the probability is 3/6 = 1/2 (the count of even numbers divided by the total count of numbers on the die)
The probability to get 1 is 1/6. The probability to get 3 is 1/6
The probability to get 3 or 1 is the sum of these two which is 1/6 + 1/6 = 2/6 = 1/3
To get a 5, rtrtthe probability is 1/6
The expected value is thus: