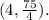To answer this question we first, have to put the length of the rectangle in terms of x. We know that the total area is 150 ft², and that the area of a rectangle is given by:
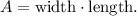
Solving the above equation for the length, and substituting width=x, and A=150, we get:
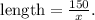
Now, the length of the interior rectangle is:
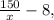
and the width of the interior triangle is:
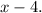
Therefore, the area of the interior triangle is given by the following expression:
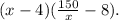
Now, to determine the domain, we know that the sides of the interior rectangle must fulfill the following inequalities:
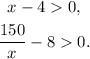
Therefore,

Answer:
Area as a function of x
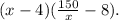
Domain: