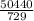
Step-by-step explanation
A geometric serie has a common ratio, the formula for the nth term is
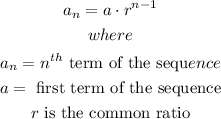
so
Step 1
find the geometric serie
a) find the common ratio
let
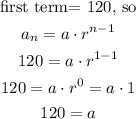
so
a=120
and
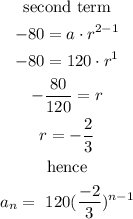
so, the sequence is
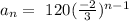
let's check
Step 2
now, let's find the sum:
the sum of geometric serie is give by
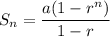
let n= 8,
replace
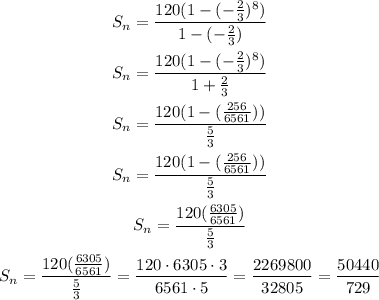
therefore, the answer is
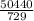
I hope this helps you