Question

What is the value of x in the equation 3^(2x-1)=27?

Answer 1

x=2

Explanation:

Given the equation:

`3^(2x-1)=27`

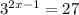
To solve for x, begin by writing 27 as a power of 3.

`3^(2x-1)=3^3`

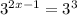
Next, since both sides of the equation have the same base, 3, it follows from the law of indices that:

`\begin{gathered} a^x=a^y\implies x=y \\ \text{Therefore:} \\ 3^(2x-1)=3^3\implies2x-1=3 \end{gathered}`

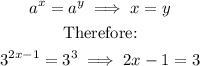
We then solve the resulting equation for x.

`\begin{gathered} 2x-1=3 \\ \text{Add 1 to both sides} \\ 2x-1+1=3+1 \\ 2x=4 \\ \text{Divide both sides by 2} \\ (2x)/(2)=(4)/(2) \\ x=2 \end{gathered}`

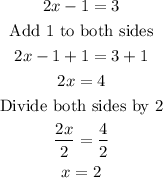
The value of x in the equation is 2.