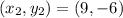We are given that the end-point of a line segment is (3, 2) and the middle point is (6, -2).
The formula for the middle point of a line segment is given by:
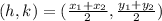
Where "h" and "k" are the middle points of the segment.
Now, we can set each of the coordinates equal. For the x-coordinates we have:
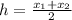
Where:
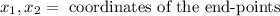
Now, we solve for the second end-point.
First, we multiply both sides by 2:
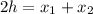
Now, we subtract x1 from both sides:

Now, we substitute both sides:
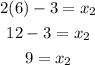
Now, we solve for the y-coordinate:
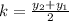
Now, we multiply both sides by 2 and subtract the first coordinate to both sides:
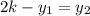
Now, we plug in the values:
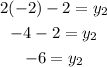
Therefore, the coordinates of the other end-point is: