The given function is
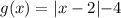
When reflected across the x-axis and translate 2 units right, and 2 units down, then its image will be
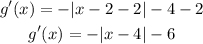
Then its maximum vertex is (4, -6)
Since the maximum value is the y-coordinate of the maximum point, then
Its maximum value is -6
From the graph, we can see that the maximum point of f(x) is (-2, -4)
Since it will translate 2 units left and 5 units up, then
Subtract 2 from the x-coordinate, and add 5 to the y-coordinate of f(x) to find the maximum point of f'(x)
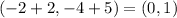
The maximum point of f'(x) is (0, 1)
The maximum value of f'(x) is 1
Since 1 > -6, then
f'(x) > g'(x)
f'(x) has a larger maximum and it is 1
The answer is C (3rd choice)