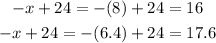Question

Sec(9x + 2) = csc(-x + 24)

Answer 1

Consider the given expression,

`\begin{gathered} \sec (9x+2)=\csc (-x+24) \\ \sec (9x+2)=\csc (24-x) \end{gathered}`

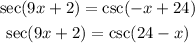
Consider the formulae,

`\begin{gathered} \sec \theta=(1)/(\cos\theta) \\ \csc \theta=(1)/(\sin\theta) \\ \sin (90-\theta)=\cos \theta \end{gathered}`

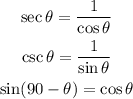
Then the expression is transformed as,

`\begin{gathered} (1)/(\cos(9x+2))=(1)/(\sin (24-x)) \\ \sin (24-x)=\cos (9x+2) \\ \sin (24-x)=\sin \mleft\lbrace90-(9x+2)\mright\rbrace \\ \sin (24-x)=\sin \lbrace90-9x-2\rbrace \\ 24-x=88-9x \\ 9x-x=88-24 \\ 8x=64 \\ x=8 \end{gathered}`

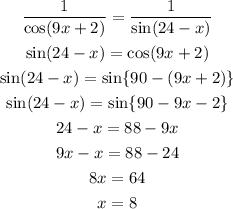
Consider another formula,

`\sin (90+\theta)=\cos \theta`

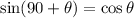
This will give the other value of 'x',

`\begin{gathered} (1)/(\cos(9x+2))=(1)/(\sin(24-x)) \\ \sin (24-x)=\cos (9x+2) \\ \sin (24-x)=\sin \mleft\lbrace90+(9x+2)\mright\rbrace \\ 24-x=90+9x+2 \\ 9x+x=24-88 \\ 10x=-64 \\ x=-6.4 \end{gathered}`

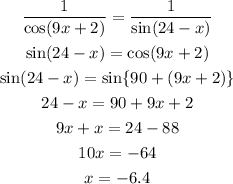
Thus, the given trigonometric equation has two solutions 8 and -6.4

Solve for the first angle as,

`\begin{gathered} 9x+2=9(8)+2=72+2=74 \\ 9x+2=9(-6.4)+2=-57.6+2=-55.6 \end{gathered}`

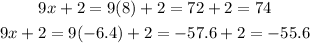
Solve for the other angle as,

`\begin{gathered} -x+24=-(8)+24=16 \\ -x+24=-(6.4)+24=17.6 \end{gathered}`