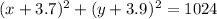The standard circle equation is
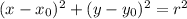
Where r is the radius of the circle, and O = (x₀, y₀) is the center of the circle.
In our problem, the radius is 32, and the center of the circle is (-3.7, -3.9), then we have
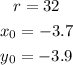
Now we just have to put these values on our circle equation
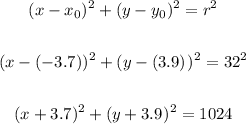
The standard form of the equation is