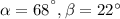
1) We can tackle this question by setting a system of Linear equations for these angles.
2) Let's set that and solve it by the Method of Elimination.
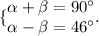
Note that we are considering the same angles from the 1st equation as in the second. The 1st equation is the definition of complementary angles.
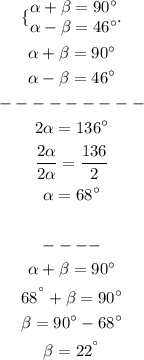
Note that after finding alpha we could plug into one of those equations and find beta.
Thus that's the answer.