Question

The sum of the measures of any two complementary angles is 90°. The differencebetween the measures of two specific complementary angles is 46. What is themeasure of each angle? Enter them below, separated by a comma. Write "deg" for thedegree symbol.Pls see the picture

Answer 1

`\alpha=68^{^(\circ)},\beta=22^(\circ)`

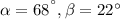
1) We can tackle this question by setting a system of Linear equations for these angles.

2) Let's set that and solve it by the Method of Elimination.

`\mleft\{\begin{matrix}\alpha+\beta=90^(\circ) \\ \alpha-\beta=46^(\circ)\end{matrix}\mright.`

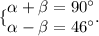
Note that we are considering the same angles from the 1st equation as in the second. The 1st equation is the definition of complementary angles.

`\begin{gathered} \mleft\{\begin{matrix}\alpha+\beta=90^(\circ) \\ \alpha-\beta=46^(\circ)\end{matrix}\mright. \\ \alpha+\beta=90^(\circ) \\ \alpha-\beta=46^(\circ) \\ --------- \\ 2\alpha=136^(\circ) \\ (2\alpha)/(2\alpha)=(136)/(2) \\ \alpha=68^(\circ) \\ \\ ---- \\ \alpha+\beta=90^(\circ) \\ 68^{^(\circ)}+\beta=90^(\circ) \\ \beta=90^(\circ)-68^(\circ) \\ \beta=22^{^(\circ)} \end{gathered}`

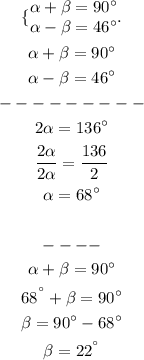
Note that after finding alpha we could plug into one of those equations and find beta.

Thus that's the answer.