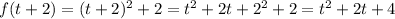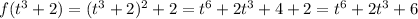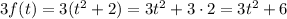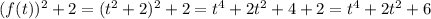Consider the function f(x) = (x)^2+2 which is equivalent to the given function. In here, we are taking whatever is inside the the parenthesis , we raise it to the power of 2 and then add 2. Note that if we change the x for a t, we will get f(t) = (t)^2+2 which is essencially the same thing.
To solve this question we will use the following formula
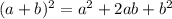
So, now we simply replace and simplify: