So first of all let's rewrite the inequalities. The first one is:
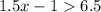
We can add 1 at both sides of it:
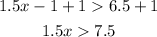
And we can divide both sides by 1.5:
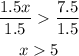
So this inequality can be written as x>5. The second one is:

We substract 3 from both sides:
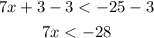
And we divide both sides by 7:
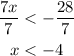
So the inequalities are x>5 and x<-4. This means that the parts of the number line that must be colored are those at the right of 5 (according to the first inequality) and at the left of -4 (according to the second). Since the inequalities use the siymbols "smaller than" and "greater than" with no equals there must be blank dots at -4 and 5. The option that meets all these conditions is the second which is the answer.