Question

a positive real number is 4 less than another. If the sum of the square of the two numbers is 62, find the numbers.

Answer 1

We have two positive numbers x and y.

We know that x is 4 less than y, so we can write:

`x=y-4`

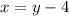
We know that the sum of the square of the two numbers is 62, so we can write:

`x^2+y^2=62`

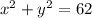
If we replace x with y we can find the value of y as:

`\begin{gathered} x^2+y^2=62 \\ (y-4)^2+y^2=62 \\ (y^2-8y+16)+y^2=62 \\ 2y^2-8y+16-62=0 \\ 2y^2-8y-^{}46=0 \\ 2(y^2-4y-23)=0 \\ y^2-4y-23=0 \end{gathered}`

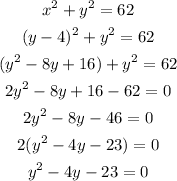
We have to calculate the roots of y:

`\begin{gathered} y=\frac{-(-4)\pm\sqrt[]{(-4)^2-4\cdot1\cdot(-23)}}{2\cdot1} \\ y=\frac{4\pm\sqrt[]{16+92}}{2} \\ y=\frac{4\pm\sqrt[]{108}}{2} \\ y\approx(4\pm10.4)/(2) \\ y_1\approx(4-10.4)/(2)=-3.2\longrightarrow\text{Not valid (it has to be positive)} \\ y_2\approx(4+10.4)/(2)=(14.4)/(2)=7.2 \end{gathered}`

The value of y is 7.2.

Then, the value of x is 7.2 - 4 = 3.2.

We can check the squares as:

`\begin{gathered} x^2+y^2 \\ 3.2^2+7.2^2 \\ 10.24+51.84 \\ 62.08 \end{gathered}`

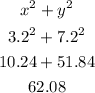
The difference between 62.08 and 62 is an error of approximation when rounding the square root of 108.

Answer: the numbers are approximately 3.2 and 7.2.