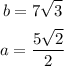Step-by-step explanation
First triangle
Since it is a right triangle, we can use the trigonometric ratio tan(θ) to find the length b.
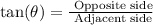
So, we have:

Second triangle
Since it is a right triangle, we can use the trigonometric ratio cos(θ) to find the length a.
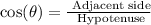
So, we have:

Answer