Solution:
Given the graph:
(a) The coordinates of P(x,y) and Q(x,y) are;
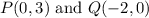
(b) The gradient, m of the line segment is;
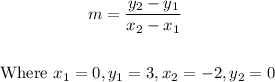
Thus;

(c) The equation of the line is;
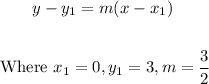
Thus;
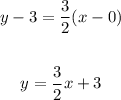
(d) The length of the line segment PQ is;
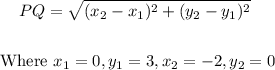
Thus;
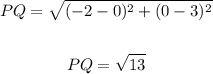
(e) The midpoint, MP of the line segment is;
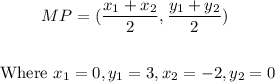
Thus;
