Question

Finding area of triangle with one side being a radical.

Answer 1

Given:

Length of one side of square = 4

Length of one side of triangle = 7

Let's find the area of the triangle.

Let's find the diagonal which is the base of the triangle.

Apply Pythagorean Theorem to find the diagonal.

We have:

`\begin{gathered} c=√(4^2+4^2) \\ \\ c=√(16+16) \\ \\ c=√(32) \\ \\ c=√(2*16) \\ \\ c=4√(2) \end{gathered}`

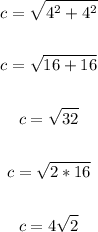
Now, to find the area, apply the formula:

`A=(1)/(2)*b*h`

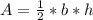
Where:

is the area

b is the base = 4√2

h = 7

Thus, we have:

`\begin{gathered} A=(1)/(2)*4√(2)*7 \\ \\ A=14√(2) \\ \\ A=19.8 \end{gathered}`

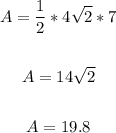
The area of the triangl is 19.8 square units.

Now, to find the primetrer, let's find the hypotenuse using the Pythagorean Theorem:

`\begin{gathered} c=\sqrt{7^2+(4√(2))^2} \\ \\ c^=√(49+32) \\ \\ c=√(81) \\ \\ c=9 \end{gathered}`

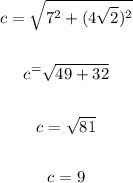
Now, to find the perimeter of the triangle, we have:

`\begin{gathered} P=4√(2)+7+9 \\ \\ P=5.7+7+9 \\ \\ P=21.7 \end{gathered}`

Therefore, the perimeter of triangle 21.7 units.

ANSWER:

• Area = 19.8 square units

,

• Perimeter = 21.7 units