Make a right triangle using the point on the terminal arm in standard position.
Find the length of the hypotenuse using pythagorean theorem
![\begin{gathered} c^2=a^2+b^2 \\ c^2=(-8)^2+(7)^2 \\ c^2=64+49 \\ c^2=113 \\ c=\sqrt[]{113} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gdyi2y11rcq1qz5zblv7ne0xmtv04c4cqz.png)
Recall the three primary trigonometric ratios
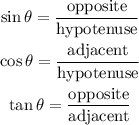
The opposite side of angle θ is -8.
The adjacent side of angle θ is 7
The hypotenuse is square root of 113.
Substitute the following to get their ratios
![\begin{gathered} \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}}=\frac{-8}{\sqrt[]{113}} \\ \text{rationalize and this becomes} \\ \frac{-8}{\sqrt[]{113}}\cdot\frac{\sqrt[]{113}}{\sqrt[]{113}}=\frac{-8\sqrt[]{113}}{113} \\ \sin \theta=\frac{-8\sqrt[]{113}}{113} \\ \\ \cos \theta=\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{7}{\sqrt[]{113}} \\ \text{rationalize the ratio and this becomes} \\ \frac{7}{\sqrt[]{113}}\cdot\frac{\sqrt[]{113}}{\sqrt[]{113}}=\frac{7\sqrt[]{113}}{113} \\ \cos \theta=\frac{7\sqrt[]{113}}{113} \\ \\ \tan \theta=\frac{\text{opposite}}{\text{adjacent}}=(-8)/(7) \\ \tan \theta=(-8)/(7) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gv8c5vmmn9o7l2ygz0oer4xdhjek4bk8bs.png)
The reciprocal of the primary trigonometric ratios are the following
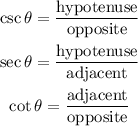
Do the same with the previous ratios, and substitute to get their ratios
![\begin{gathered} \csc \theta=\frac{\text{hypotenuse}}{\text{opposite}}=\frac{\sqrt[]{113}}{-8} \\ \csc \theta=-\frac{\sqrt[]{113}}{8} \\ \\ \sec \theta=\frac{\text{hypotenuse}}{\text{adjacent}}=\frac{\sqrt[]{113}}{7} \\ \sec \theta=\frac{\sqrt[]{113}}{7} \\ \\ \cot \theta=\frac{\text{adjacent}}{\text{opposite}}=(7)/(-8) \\ \cot \theta=-(7)/(8) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/o3gfxm5gqr1evrb1ngyfmidmonte9tzvos.png)