We want to calculate the image of (4,8). So first we identify that line m is line y=2.
To reflect the point around the line m, we need to find the distance between point (4,8) and line y=2. To do so, we will draw a vertical line that passes through point (4,8) and check where it crosses the line y=2. So the line would look like this.
Now, we want to calculate the distance between this two points. To do so, we will use the formula
![d=\sqrt[]{(a-c)^2+(b-d)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/ntncn764c6tki92xvoexvpy095nt5whfx2.png)
which would be tghe distance between points (a,b) and (c,d). So using the formula to points (4,8) and (4,2) we get
![d=\sqrt[]{(8-2)^2+(4-4)^2}=\sqrt[]{(8-2)^2}=(8-2)=6](https://img.qammunity.org/2023/formulas/mathematics/college/locemmiffcycq3pzh7ocp16f9ov2mjytu2.png)
Now, we want to find a point over the blue line that is at distance 6 from the red line, but is under the red line. We achieve this by taking the point of intercsection (4,2) and subtract 6 on the y coordiante. So the reflection of point (4,8) on line m is simply given by the point
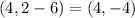
So the reflection of point (4,8) on line m is the point (4,-4).
Now, we want to reflect (4,-4) on line n. First we identify that the vertical line n is the line x=3. Now, we repeat the process as before.
In this case, we draw a horizontal line to identify the point of intersection, it would be
NOw, we calculate the distance. As they are on a horizontal line, we can simply subtract the x coordiantes and then take the absolute value.
This leads to

So know we subtract the distance from the x coordinate of the intersection. We get
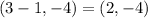
So the reflection of point (4,-4) on line n is (2,-4)