Question

If the hydraulic lift in question 1 needs to lift a car with a weight of 6000 N, what is the surface area of the lifting platform to balance the pressures?Question 1 for reference:1.If a hydraulic lift uses a force of 400 N on a piston of area 0.065 m2, what is the pressure on the piston? (10 points) Approximately 6153.84 Pa

Answer 1

Given:

Piston 1 has an area

`A_1=0.065\text{ m}^2`

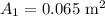
and the force applied on this piston is

`F_1=\text{ 400 N}`

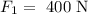
The force on piston 2, which is the weight of the car, is

`F_2=6000\text{ N}`

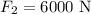
Required: The area of piston 2.

Step-by-step explanation:

The formula that can be obtained by balancing the pressures is

`\begin{gathered} P_1=P_2 \\ (F_1)/(A_1)=(F_2)/(A_2) \\ A_2=(F_2A_1)/(F_1) \end{gathered}`

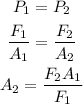
On substituting the values, the area of the second piston will be

`\begin{gathered} A_2=(6000*0.065)/(400) \\ =0.975\text{ m}^2 \end{gathered}`

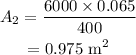
Final Answer: The area of the piston lifting the car is 0.975 meter-squared.