Question

X varies directly with the square of y, where x>0,and y >0. If x = 3 when y = 5, then what is the valueof y when x = 48?

Answer 1

x varies directly with y²

You can express this relationship as:

`x=ky^2\text{ }\forall x>0,y>0`

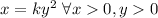
Where k is the coefficient of variation.

Using the values of x=3 and y=5 you can calculate the coefficient of variation k:

`\begin{gathered} 3=k(5)^2 \\ 3=k\cdot25 \\ k=(3)/(25) \\ k=0.12 \end{gathered}`

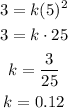
So the equation of the relationship is:

`x=0.12y^2`

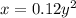
With this you can calculate y when x=48 as:

`\begin{gathered} 48=0.12y^2 \\ (48)/(0.12)=(0.12y^2)/(0.12) \\ 400=y^2 \\ y=\sqrt[]{400} \\ y=20 \end{gathered}`

So for this relationship, when x=48, y=20