Question

When looking at a rational function f(x) = (x+3)(x-2)(x+5) ——————— (x-3)(x+2)(x-5), Charles and Bobby have two different thoughts. Charles says that the function is defined at x = - 2, x = 3, and x = 5. Bobby says that the function is undefined at those x values. Who is correct? Justify your reasoning.

Answer 1

We have on the denominator the next expression:

`(x-3)(x+2)(x-5)`

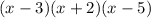
The function is not defined when the denominator is equal to 0.

`(x-3)(x+2)(x-5)\\e\text{ 0}`

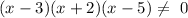
So the function is undefined when

x-3 =0

x+2=0 and

x-5 = 0

Solving for x:

x=3

x=-2

x=5.

With the before information, we can find that Bobby is right, the function is undefined when x=3. x=-2 and x=5.