Step-by-step explanation
We are given the following information:
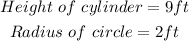
We are required to determine the following:
• The lateral area.
,
• Single base area.
,
• Surface area.
The lateral area can be calculated as:

Hence, the lateral area is 113.14 ft².
The single base can be calculated as:
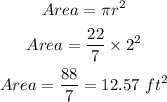
Hence, the single base area is 12.57 ft².
Therefore, the surface area can be calculated as:
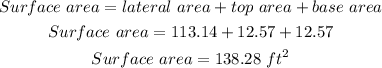
Hence, the surface area is 138.28 ft².