Question

Using the Cylinder in the picture, find the Lateral Area, the Area of a Single Base, and the TOTAL Surface Arhundredth)2 ft-9 ftLateral Area =Single Base Area =Surface Area =Blank 1:Blank 2:Blank 3:ft²ft²ft²

Answer 1

Step-by-step explanation

We are given the following information:

`\begin{gathered} Height\text{ }of\text{ }cylinder=9ft \\ Radius\text{ }of\text{ }circle=2ft \end{gathered}`

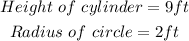
We are required to determine the following:

• The lateral area.

,

• Single base area.

,

• Surface area.

The lateral area can be calculated as:

`\begin{gathered} Lateral\text{ }Area=2\pi rh \\ Lateral\text{ }Area=2*(22)/(7)*2*9 \\ Lateral\text{ }Area=(792)/(7)=113.14\text{ }ft^2 \end{gathered}`

Hence, the lateral area is 113.14 ft².

The single base can be calculated as:

`\begin{gathered} Area=\pi r^2 \\ Area=(22)/(7)*2^2 \\ Area=(88)/(7)=12.57\text{ }ft^2 \end{gathered}`

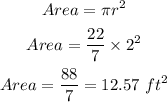
Hence, the single base area is 12.57 ft².

Therefore, the surface area can be calculated as:

`\begin{gathered} Surface\text{ }area=lateral\text{ }area+top\text{ }area+base\text{ }area \\ Surface\text{ }area=113.14+12.57+12.57 \\ Surface\text{ }area=138.28\text{ }ft^2 \end{gathered}`

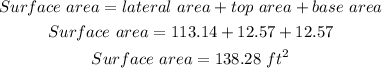
Hence, the surface area is 138.28 ft².