Answer:
6%
Explanation:
The marked price of the electric heater = Rs 4000
• In winter, when 10% discount was given, the retailer made 20% profit.
• In summer, ,when the discount was increased by x%,, the retailer made 12% profit.
We want to find the value of x.
First, we find the sale price of the good after a 10% discount.
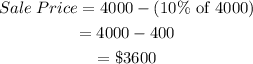
Next, the retailer made a 20% profit when he sold the heater at $3600, we find the cost price of the heater.

The cost price of the water heater is Rs 3000.
In the summer, she increased the discount percent to get only 12% profit from the same type of heater.
We find the selling price that gives a 12% profit.

The selling price in summer was $3,360.
Finally, we find the discount.
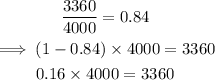
The new discount was 16%.
Therefore:
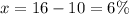
The retailer increased the discount by 6%.