1)
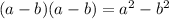
we can use the distribution propertie:
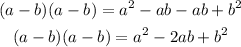
Is false
2)
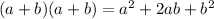
Again, we can use the distribution propertie:
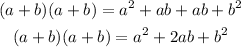
Is true
3) is the same as the numeral 1) so in this case the experession is true
4)
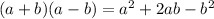
Again, we can use the distribution propertie:
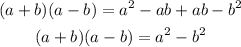
Is false
5) is the same as the numeral 4) so in this case is true
6)
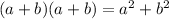
Using the distribution:
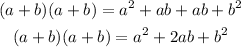
So is false