The slopes of the asymptotes,
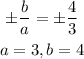
Then
the coordinates of the foci have
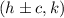
Since the coordinate of one focus is
![\begin{gathered} (-4,5) \\ \text{thus, } \\ h\pm c=-4 \\ \text{from} \\ c^2=a^2+b^2 \\ a=3,b=4 \\ c^2=9+16=25 \\ c=\sqrt[]{25}=\pm5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zuepujx7bt7djcppq18kahpzu6t6d466wk.png)
then equate
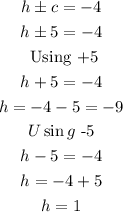
Using the coordinates of the centre from the above values of h are
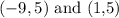
The coordinate of the center that will give a vertex of (-2,5) is (1,5)
Hence, the final answer is ( 1 , 5 )