Figure 2 is the image of Figure 1 after rotation by an angle of 90degrees counter-clockwise
Step 1: Write out the coordinates of EFGH and the coordinates of KLMN,


Step 2: Write out the formula for the rotation of a point (x,y) by 90° counter-clockwise
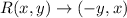
Step 3: Show that the points KLMN are the images of R on EFGH
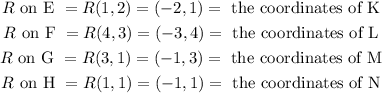
Hence, Figure 2 is the image of Figure 1 on Rotation by 90 degrees counter-clockwise
Since rotation preserves the shape of a figure, then the measures of corresponding angles are equal.
Therefore,
m
The third Choice is correct