Question

Jose has $25 to spend on gas. Gas cost $1.25 per gallon. This situation is modeled by the function, M(g) = 25 -1.25g, where Mg) represents the amount of money Jose has remaining as a function of the number of gallons of gas, g he pumped. Which inequality represents the situational domain and range?

Answer 1

Domain: 0 ≤ x ≤ 20

Range: 0 ≤ y ≤ 25

Step-by-step explanation:

Given:

Amount he has to spend on gas = $25

Cost of gas per gallon = $1.25

M(g) = 25 -1.25g

Josh will buy a maximum of 20 gallons of gas.

`i\mathrm{}e\text{ }(25)/(1.25)\text{ = 20}`

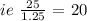
Thus,

M(20) = 25 - 1.25(20)

= 25 - 25

= 0

To domain will be the set of input values while the range will be the ouput values.

The domain will be all real values ranging from 0 to 20,

The inequality that represents domain =

0 ≤ x ≤ 20

The inequality that represents range =

0 ≤ y ≤ 25