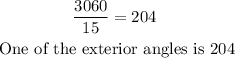Answer:
Explanation:
The interior angles of any polygon are represented by the following equation:
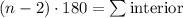
If the sum of the interior angles is 2340, solve for n to determine how many vertices it has:
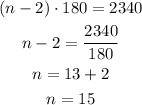
Now, if the polygon has 15 vertices. Use the equation for the sum of exterior angles, which is represented as:

If it is a regular polygon, each angle measures the same: