Question

How much money should be deposited today in an account that earns 5.5% compounded monthly so that it will accumulate to 11,000 in three years?

Answer 1

$9,330.35

Step-by-step explanation:

We'll use the below compound interest formula to solve the problem;

`A=P(1+(r)/(n))^(nt)`

Where A = the future amount = $11,000

P = the starting amount(the principal)

r = the interest rate in decimal = 5.5% = 5.5/100 = 0.055

n = number of compounding periods = 12

t = time periods = 3 years

So let's go ahead and substitute the above values into our equation;

`11000=P(1+(0.055)/(12))^(12\ast3)`

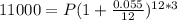
We can then evaluate and find P;

`\begin{gathered} 11000=P(1.004583)^(36) \\ 11000=P(1.178949) \\ P=(11000)/(1.178949) \\ \therefore P=9,330.35 \end{gathered}`

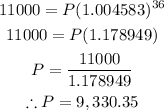
So the amount that should be deposited is $9,330.35