To calculate the perpendicular slope, the steps are the following:
• Step 1: Find the original slope of the line
,
• Step 2: Use the condition for the perpendicular slope, to find the perpendicular slope.
Step 1. To find the slope of the given line
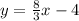
we need to compare this with the slope-intercept equation

where m is the slope and b is the y-intercept of the line. Thus, we can see that the number that accompanies the x represents the slope. And in this line
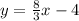
That number is 8/3. I will call this the slope m1:
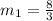
Step 2. The condition for two lines m1 and m2 to be perpendicular is:
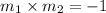
Since in this case we know the original slope m1, and we are looking for perpendicular slope m2, we substitute m1, and solve for m2:

Solving for m2, we need to multiply each side of the equation by 3/8:
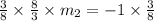
On the left side we are only left with m2, and on the right side we are left with -3/8:
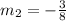
Answer: -3/8