Question

Find the relative extrema of the function and classify each as a maximum or minimum. s(x) = -x2 - 6x + 112 Relative maximum: (-6, 112) Relative maximum:(-3, 121) Relative maximum: (3, 121) Relative minimum: (6, 112)

Answer 1

To find the relative extrema of the function

`s(x)=-x^2-6x+112`

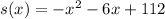
We need to find the derivative of the function, then

`(ds)/(dx)=-2x-6`

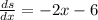
Then we equate the derivative to zero and solve for x:

`\begin{gathered} (ds)/(dx)=0 \\ -2x-6=0 \\ -2x=6 \\ x=-(6)/(2) \\ x=-3 \end{gathered}`

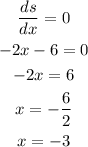
Therefore we have a relative extrema at x=-3 with value s=121.

Now we need to find out if this value is a maximum or minimum, to do that we need to find the derivative of the derivative.

`\begin{gathered} (d)/(dx)((ds)/(dx))=(d)/(dx)(-2x-6) \\ =-2 \end{gathered}`

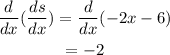
Since the value of the second derivative is negative for every value of x, the relative extrema is a maximum.

Therefore we have a maximum at the point (-3,121).