To find the relative extrema of the function

We need to find the derivative of the function, then
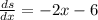
Then we equate the derivative to zero and solve for x:
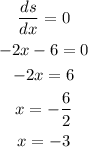
Therefore we have a relative extrema at x=-3 with value s=121.
Now we need to find out if this value is a maximum or minimum, to do that we need to find the derivative of the derivative.

Since the value of the second derivative is negative for every value of x, the relative extrema is a maximum.
Therefore we have a maximum at the point (-3,121).