Question

Jenny's school is selling tickets to a play. On the first day of ticket sales the school sold 6 adult tickets and 4 student tickets for a total of $100. The school took in $90 on the second day by selling 5 adult tickets and 5 student tickets. What is the price of one student ticket? $4 $5 $11 $14

Answer 1

Given :

The number of tickets sold in the first day : 6 adult tickets and 4 student for a total of $100.

In the second day : 5 adults and 5 students fro $90

Let the price of the adult tickets = x

And the price of the student tickets = y

So, we have the following system of equations :

`\begin{gathered} 6x+4y=100\rightarrow(1) \\ 5x+5y=90\rightarrow(2) \end{gathered}`

For the question (2), divide all terms by 5 then solve the equation for x

`\begin{gathered} (5x)/(5)+(5y)/(5)=(90)/(5) \\ \\ x+y=18 \\ x=18-y \end{gathered}`

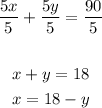
Substitute with x in the first equation :

`\begin{gathered} 6(18-y)+4y=100 \\ 108-6y+4y=100 \\ -2y=100-108 \\ -2y=-8 \\ \\ y=(-8)/(-2)=4 \end{gathered}`

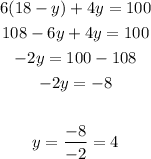
So, the price of the student ticket = $4