How many positive integers x satisfy the inequality ?100 \leqslant {x}^(2) \leqslant 200

Question

How many positive integers x satisfy the inequality ?
`100 \leqslant {x}^(2) \leqslant 200`

Answer 1

5 positive integers

Explanation:

We have the following inequality:

`100\le x^2\le200`

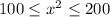
Solving for x:

`\begin{gathered} \sqrt[]{100}\le\sqrt[]{x^2}\le\sqrt[]{200} \\ \pm10\le x\le\pm10\sqrt[]{2} \end{gathered}`

Being only positive numbers, it would then remain:

`10\le x\le10\sqrt[]{2}`

Being only integers, it would then remain:

`\begin{gathered} 10\le x\le10\sqrt[]{2} \\ 10\sqrt[]{2}=14.14\cong14 \\ \text{therefore:} \\ 10\le x\le14 \\ x=10,11,12,13,14 \end{gathered}`

Which means that 5 positive integers satisfy the inequality (10, 11, 12, 13, 14)