Step 1: Problem
Find E and find F to the nearest degree and find DF to the nearest tenth.
Step 2: Concept
1. Apply sine and cosine formula to find the angle E and F
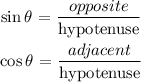
2. Apply Pythagoras theorem to find length DF

Step 3:
For angle F
Opposite = 5
Hypotenuse = 5.83

For angle E
adjacent = 5
hypotenuse = 5.83

Hypotenuse = 5.85 ft
Opposite = 5ft
Adjacent = DF
![\begin{gathered} \text{Opposite}^2+Adjacent^2=Hypotenuse^2 \\ 5^2+DF^2=5.83^2 \\ 25+DF^2\text{ = 33.9889} \\ DF^2\text{ = 33.9889 - 25} \\ DF^2\text{ = 8.9889} \\ DF\text{ = }\sqrt[]{8.9889} \\ DF\text{ = 2.998} \\ DF\text{ = 3.0} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/331568pvnit3u09tatn67meiypcntrlo6a.png)
Step 4: Final answer
Angle F = 59
Angle E = 31
Length DF = 3.0