Question

Find E and find F to the nearest degree and find DF to the nearest tenth.

Answer 1

Step 1: Problem

Find E and find F to the nearest degree and find DF to the nearest tenth.​

Step 2: Concept

1. Apply sine and cosine formula to find the angle E and F

`\begin{gathered} \sin \theta\text{ = }\frac{opposite}{\text{hypotenuse}} \\ \cos \theta\text{ = }\frac{adjacent}{\text{hypotenuse}} \end{gathered}`

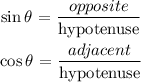
2. Apply Pythagoras theorem to find length DF

`\text{Opposite}^2+Adjacent^2=Hypotenuse^2`

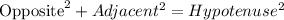
Step 3:

For angle F

Opposite = 5

Hypotenuse = 5.83

`\begin{gathered} \sin F\text{ = }\frac{Opposite}{\text{Hypotenuse}} \\ \sin F\text{ = }(5)/(5.83) \\ \sin F\text{ = 0.857632} \\ F\text{ = }\sin ^(-1)0.857632 \\ F\text{ = 59.05} \\ F\text{ = 59} \end{gathered}`

For angle E

adjacent = 5

hypotenuse = 5.83

`\begin{gathered} \cos E\text{ = }\frac{adjacent}{\text{hypotenuse}} \\ \cos E\text{ = }(5)/(8.83) \\ \cos E\text{ = 0.857632} \\ E\text{ = }\cos ^(-1)0.857632 \\ E\text{ = 30.9} \\ E\text{ = 31} \end{gathered}`

Hypotenuse = 5.85 ft

Opposite = 5ft

Adjacent = DF

`\begin{gathered} \text{Opposite}^2+Adjacent^2=Hypotenuse^2 \\ 5^2+DF^2=5.83^2 \\ 25+DF^2\text{ = 33.9889} \\ DF^2\text{ = 33.9889 - 25} \\ DF^2\text{ = 8.9889} \\ DF\text{ = }\sqrt[]{8.9889} \\ DF\text{ = 2.998} \\ DF\text{ = 3.0} \end{gathered}`

Step 4: Final answer

Angle F = 59

Angle E = 31

Length DF = 3.0