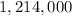Let P be the initial population of mosquitoes for a given year. Let k be the percentual increase of the population over a year.
To calculate the population after a year, first calculate the increase by multiplying k times P:
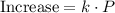
Add the increase to the initial population to know the population after a year:
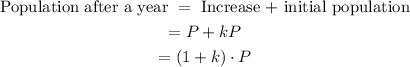
Therefore, to calculate the population after a year, we have to multiply the initial population by (1+k).
To calculate the population after two years, take (1+k)P as the new initial population:
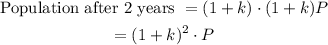
By analogy, after n years, the population will be equal to:
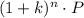
Since 5 years pass from 2003 to 2008, the initial population was 800,000 and the yearly percentual increase is 8.7%, then n=5, P=800,000 and k=8.7/100. Substitute in the formula to know the population of mosquitoes in 2008:
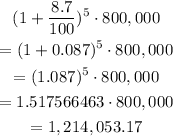
Therefore, the population of mosquitoes in the park in 2008 will be approximately (to the nearest tousand):